Hashing 3D space
One of the challenges when dealing with 3D objects is a spatial partitioning. A common problem is to find an object in a specified area or a nearest object. Typically we divide the space into cells and reduce the problem to searching for a cell containing a point or an object.
Example of Octree cells
But what if we are looking for objects that are close together? Can we still use cells effectively? The answer is no. We still can enumerate all objects within one cell however we won't get easily closest objects from surrounding cells.
Consider this example with two cells:
cell0 = {a, b} // cell0 contains 2 points a and b
cell1 = {c} // cell1 contains 1 point c
r is a proximity radius
All points {a, b, c} are in proximity radius r but belong to two different cells.
r is a proximity radius
All points {a, b, c} are in proximity radius r but belong to two different cells.
2 cells with points within radius
In general we are looking for objects having similar properties like the distance. This problem is more common in large databases when searching for similar items and is known as Nearest Neighbour Search. One of the possible solution is called Locality Sensitive Hashing.
Locality Sensitive Hashing
Locality Sensitive Hashing (LSH) introduces a hash function that maps similar items to the same bucket with high probability. In contrast to the traditional hash function the number of buckets is smaller than the number of input items and the goal is to maximize the probability of a collision for similar items.
LSH hash function is defined as:
l s h
:
M
→
B
, e v e r y
p o i n t f r o m
m e t r i c s p a c e m
∈
M
m a p s t o b u c k e t b
∈
B
let R > 0 be a threshold,
two points m0 and m1 belongs to the same bucket b if d(m0, m1) ≤ R,
where d is a distance function
Hamming or Euclidean distance is typically used as a distance function. Finding a good threshold R depends on application and distributions of elements. High threshold could lead to fewer buckets and high collisions but also low quality similarities.
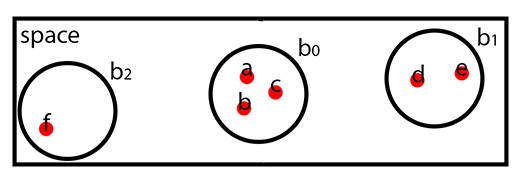
Let's get back to the example. LSH-hashed objects in the space can look like in the next picture. Points {a, b, c} belong to the bucket b0, points {d, e} to b1 and the point {f} to bucket b2.
where d is a distance function
Hamming or Euclidean distance is typically used as a distance function. Finding a good threshold R depends on application and distributions of elements. High threshold could lead to fewer buckets and high collisions but also low quality similarities.
Let's get back to the example. LSH-hashed objects in the space can look like in the next picture. Points {a, b, c} belong to the bucket b0, points {d, e} to b1 and the point {f} to bucket b2.
LSH-hashed objects
Application
LSH was successfully used in a real-time mesh explosion system Exploder for Unity Game Engine which I made around 2 years ago. This system is capable of cutting 3D mesh into hundreds of pieces in the matter of milliseconds. The biggest challenge here was to find a contour of cut object as quickly as possible and pass it to triangulation phase. The traditional approach is to prepare a 3D mesh in some heavy data structure like half-edge however it is not quite suitable for real-time processing for it's memory footprint.
All points on cut plane were LSH-hashed into buckets {b0...bn} and it was possible to do very fast look-ups of 3D points and search for contours. Another benefit was that the points belonging to the same bucket (within small proximity) were actually filtered out and treated as one point. That made things faster on complex meshes.
From a performance stand point LSH has very small memory requirements, there is no need for space subdivision, every bucket is encoded as 32-bit number and the hash function requires only a comparison of points distances, which can be done on the fly so no preprocessing is needed.
Demonstration of Exploder system.
Conclusion
LSH is a good example of a system that can be used for applications outside of its domain. Hashing of objects based on probability of collision is more common for searching of similar items like images, web or other media files. It shows that the statistical approach can be used with a great success in areas where the precision of geometry algorithms is preferred.
References
[1] Wikipedia, https://en.wikipedia.org/wiki/Locality-sensitive_hashing